EMT (Euler Math Toolbox) está diseñado para todo aquel que frecuentemente realiza operaciones de matemática numérica, optimización, estadística, matemáticas simbólicas desde nivel de estudiante hasta nivel de investigación de una manera interactiva con agradables gráficos.
Euler Math Toolbox (EMT), es un poderoso programa de matemáticas que combina herramientas numéricas y simbólicas (usando el sistema de álgebra de computadora Maxima) en un paquete gratuito y de código abierto. Su idea es similar a Matlab, pero la sintaxis no es exactamente compatible. El proyecto fue iniciado en 1987 por Rene Grothmann, profesor de matemáticas en Eichstätt, Alemania, y se convirtió en un paquete completo para la exploración matemática y la enseñanza a lo largo de los años.
El objetivo principal del diseño de Euler Math Toolbox es proporcionar una superficie limpia y simple que brinde fácil acceso a herramientas potentes.
Euler Math Toolbox es de uso gratuito para cualquier persona sin costos ni lealtades bajo la licencia GPL. También es un programa de código abierto, alojado en SourceForge y admite la idea de software abierto y bibliotecas.
El programa se ejecuta en Windows 7, 8 o 10, 32 bits o 64 bits. La versión más reciente solo admite Windows 8 o superior con 64 bits, y la versión más reciente de Ubuntu a través del emulador estable de Wine.
Euler Math Toolbox es para ti si:
- está buscando un sustituto poderoso, fácil de usar y gratuito para Matlab,
- necesitas hacer álgebra simbólica o matemática numérica en escuelas o universidades,
- eres estudiante o profesor y quieres demostrar matemáticas,
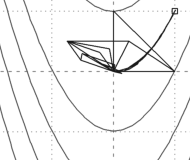
- quieres hacer bonitas ilustraciones matemáticas o incluso escenas fotográficas realistas,
En caso de que no conozca el programa y desee obtener más información sobre el programa, eche un vistazo a esta descripción general o vaya directamente al tutorial que ofrece un curso intensivo para EMT.
Tutoriales de Euler Math Toolbox:
Sintaxis y tipos de datos
- La sintaxis de Euler: contiene todo lo que necesita saber sobre la sintaxis de comandos y expresiones, incluidas las expresiones simbólicas.
- El lenguaje matricial: el lenguaje matricial es la herramienta básica para cálculos eficientes en EMT. Para obtener formas cortas y rápidas de resolver problemas, debe estar familiarizado con esta forma de manejar los cálculos numéricos.
- Números complejos: además de los números reales, EMT puede manejar números complejos, encontrar ceros de polinomios complejos y resolver ecuaciones complejas.
- Intervalos: la aritmética de intervalos, junto con el producto escalar exacto, es la herramienta principal para obtener inclusiones garantizadas para soluciones de ecuaciones lineales y no lineales o ecuaciones diferenciales.
- Maxima: este tutorial presenta expresiones simbólicas y la interfaz de Maxima. EMT incorpora a la perfección Maxima utilizando una sintaxis especial para expresiones y funciones simbólicas.
- Más sobre Maxima: algunos detalles más sobre Maxima.
Algoritmos y Funciones
- Gráficos 2D: todo sobre gráficos de una variable, curvas o gráficos implícitos en el plano.
- Gráficos 3D: todo sobre gráficos de dos variables, superficies o gráficos implícitos en el espacio 3D.
- Álgebra lineal: muestra cómo resolver sistemas lineales, calcular ajustes de mínimos cuadrados, valores propios o valores singulares, usando aritmética numérica y simbólica.
- Análisis numérico: EMT puede resolver ecuaciones y sistemas no lineales, o integrales.
- Ecuaciones diferenciales: muestra soluciones numéricas y simbólicas de ecuaciones diferenciales.
- Entrada y salida: Leer y escribir desde archivos o desde Internet.
- Estadísticas: Estadísticas es una aplicación perfecta para EMT. Este tutorial presenta distribuciones estadísticas, funciones y diagramas especiales para estadísticas. Además, muestra cómo hacer simulaciones de Monte-Carlo en EMT.
- Optimización: un tutorial sobre optimización lineal, no lineal y de enteros. EMT contiene el paquete eficiente LPSOLVE para la optimización lineal.
- Sistemas grandes: EMT puede manejar sistemas grandes y dispersos. El tutorial contiene ejemplos relacionados con la teoría de grafos.
- Transformada rápida de Fourier: esto explica FFT y cómo producir o analizar sonido en EMT.