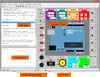
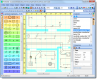
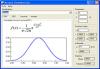
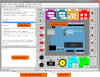
SINGULAR es un sistema algebraico por ordenador para cálculos de polinomios, con especial énfasis a las necesidades de álgebra conmutativa, geometría algebraica y la teoría de la singularidad.
Singular proporciona
- algoritmos centrales altamente eficientes,
- una multitud de algoritmos avanzados en los campos anteriores,
- un lenguaje de programación intuitivo, similar a C,
- maneras fáciles de hacerlo extensible al usuario a través de bibliotecas, y
- Un manual completo en línea y función de ayuda.
Sus principales objetos computacionales son ideales, módulos y matrices sobre una gran cantidad de baserings. Éstas incluyen
- anillos polinómicos sobre varios campos de tierra y algunos anillos (incluidos los enteros),
- localizaciones de lo anterior,
- una clase general de álgebras no conmutativas (incluyendo el álgebra exterior y el álgebra de Weyl),
- anillos de cociente de lo anterior,
- productos tensoriales de los anteriores.
Los algoritmos principales de Singular manejan
- Gröbner resp. bases estándar y resoluciones libres,
- factorización polinómica,
- resultantes, conjuntos característicos y búsqueda de raíz numérica.
Sus algoritmos avanzados, contenidos en más de 90 bibliotecas, abordan temas como la factorización absoluta, módulos D algebraicos, clasificación de singularidades, teoría de la deformación, sistemas Gauss-Manin, desarrollo de Hamburger-Noether (Puiseux), teoría invariante, (no ) álgebra homológica conmutativa, normalización, descomposición primaria, resolución de singularidades y cohomología de gavilla.