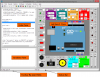
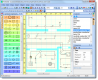
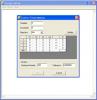
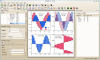
Axiom is useful for doing mathematics by computer and for research and development of mathematical algorithms. Axiom defines a strongly typed, mathematically correct type hierarchy. Axiom has a programming language and a built-in compiler.
Axiom is a general purpose Computer Algebra system. It is useful for research and development of mathematical algorithms. It defines a strongly typed, mathematically correct type hierarchy. It has a programming language and a built-in compiler.
Axiom has been in development since 1971. At that time, it was called Scratchpad. Scratchpad was a large, general purpose computer algebra system that was originally developed by IBM under the direction of Richard Jenks. The project started in 1971 and evolved slowly. Barry Trager and James Davenport were key to the technical direction of the project. Scratchpad developed over a 20 year period and was considered a research platform for developing new ideas in computational mathematics. In the 1990s, as IBM's fortunes slid, the Scratchpad project was renamed to Axiom, sold to the Numerical Algorithms Group (NAG) in England and became a commercial system. As part of the Scratchpad project at IBM in Yorktown Tim Daly worked on all aspects of the system and eventually helped transfer the product to NAG. For a variety of reasons it never became a financial success and NAG withdrew it from the market in October, 2001.
NAG agreed to release Axiom as free software. The basic motivation was that Axiom represents something different from other programs in a lot of ways. Primarily because of its foundation in mathematics the Axiom system will potentially be useful 30 years from now. In its current state it represents about 30 years and 300 man-years of research work. To strive to keep such a large collection of knowledge alive seems a worthwhile goal.
Efforts are underway to extend this software to
- Develop a better user interface
- Make it useful as a teaching tool
- Integrate additional mathematics
- Rebuild the algebra in a literate programming style
- Prove Axiom correct